Introducing CloneExtensions .NET cloning library

Blog has been moved to new address: marcinjuraszek.com. You'll be redirected to new site in few seconds. If you don't want to wait click here: Introducing CloneExtensions .NET cloning library

I've spent last two days working on my first open source .NET library named CloneExtensions. It gives you a smart way to clone your object instances without implementing any interface writing any additional Clone method at all. It uses Expression Tree to compile that Clone method for you right before you're trying to use GetClone<T> for given type T for the first time.

Project is in early phase but even now you can use it to clone plenty of different types:

• Primitive (int, uint, byte, double, char, etc.), known immutable types (DateTime, TimeSpan, String) and delegates (including Action<T>, Func<T1, TResult>, etc)
• Nullable<T>
• T[] arrays
• Custom classes and structs, including generic classes and structs.

Following class/struct members are cloned internally:

• Values of public, not readonly fields
• Values of public properties with both get and set accessors
• Collection items for types implementing ICollection<T>

If you're interested in how it works internally look at documentation, where Expression Tree creation logic is described with additional samples.

Because Expression once generated and compiled is used like it was written by you, starting from the second time method is used with the same T, it has the same performance as if you'd write the logic by yourself. That's why CloneExtensions is definitely faster then reflection-based solutions and is faster then serialization-based solutions when you clone more then just a couple instances of the same time.

Take a look at CloneExtensions and feel free to provide feedback to both existing solution and plans for future developments.

Partitioning the collection using LINQ: different approaches, different performance, the same result

Blog has been moved to new address: marcinjuraszek.com. You'll be redirected to new site in few seconds. If you don't want to wait click here: Partitioning the collection using LINQ: different approaches, different performance, the same result



Another blog post inspired by StackOverflow question. This time it's all about LINQ, performance and a tiny little detail, that really matters. The question itself is about yield keyword in VB.NET, but there is another, much more interesting part I'd like to examine. The algorithm quoted in the question is the key.

The idea is simple. How to partition a collection into parts with given number of elements in ever part? Algorithm presented in the question is as easy as the questions seems to be:

public IEnumerable<IEnumerable<T>> Partition<T>(IEnumerable<T> source, int size)
{
    if (source == null)
        throw new ArgumentNullException("list");

    if (size < 1)
        throw new ArgumentOutOfRangeException("size");

    int index = 1;
    IEnumerable<T> partition = source.Take(size).AsEnumerable();

    while (partition.Any())
    {
        yield return partition;
        partition = source.Skip(index++ * size).Take(size).AsEnumerable();
    }
}

Question is, it the algorithm good and efficient? It returns correct results, that's for sure. But that's not the only important part of every algorithm. Unfortunately, I must say that the algorithm is no good. To answer why it's no a good algorithm? I'd like to show you another approach on solving the same problem:

public IEnumerable<IEnumerable<T>> Partition<T>(IEnumerable<T> source, int size)
{
    var partition = new List<T>(size);
    var counter = 0;

    using (var enumerator = source.GetEnumerator())
    {
        while (enumerator.MoveNext())
        {
            partition.Add(enumerator.Current);
            counter++;
            if (counter % size == 0)
            {
                yield return partition.ToList();
                partition.Clear();
                counter = 0;
            }
        }

        if (counter != 0)
            yield return partition;
    }
}

Is has exactly the same signature and returns exactly the same results. Why is it better then? There are couple possible answers:

• because it does no use Skip/Take methods
• because it has O(n) complexity, when the other one is O(n*log(n))
• because it iterate over entire collection only once, and the other one does it multiple times

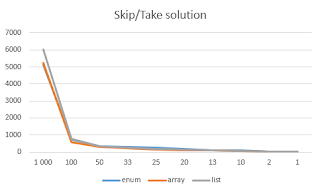
If you look closer, all these actually means the same: the second method is much faster! How much? Really much :) Look at the charts. They show execution time depending on number of partitions that need to be created. Source collections have 1000000 elements and they are created using following code:

var enumSource = Enumerable.Range(0, size);
var arraySource = enumSource.ToArray();
var listSource = arraySource.ToList();

You may wonder why I tried the same algorithm on three different collections. That's because of how Skip/Take solution works: it iterates from that beginning of collection every time new partition is requested. It may not be important if your source is static collection (like Array or List), but it will cause Enumerable.Range to generate the collection every time again and again. That's really not necessary, is it?

Y-axis shows execution time and X-axis shows number of partitions that are being generated. The difference is huge, isn't it? It takes about 6 second to generate 1000 partitions using Skip/Take algorithm and about 40ms to do that with the other one!

I'm writing this post to highlight that if LINQ seems to be really great solution for nearly every collection-related problem and you can get working solution really easily using it, it's not always really a good and fast solution.

Playing around with List<T>, part five: finding elements

Blog has been moved to new address: marcinjuraszek.com. You'll be redirected to new site in few seconds. If you don't want to wait click here: Playing around with List, part five: finding elements




This time I'll try to examine how are all search-related methods in List<T> implemented. Here is quite long list of all these methods:

public bool Exists(Predicate<T> match)
public T Find(Predicate<T> match)
public List<T> FindAll(Predicate<T> match)
public int FindIndex(Predicate<T> match)
public int FindIndex(int startIndex, Predicate<T> match)
public int FindIndex(int startIndex, int count, Predicate<T> match)
public T FindLast(Predicate<T> match)
public int FindLastIndex(Predicate<T> match)
public int FindLastIndex(int startIndex, Predicate<T> match)
public int FindLastIndex(int startIndex, int count, Predicate<T> match)
public int IndexOf(T item)
public int IndexOf(T item, int index)
public int IndexOf(T item, int index, int count)
public int LastIndexOf(T item)
public int LastIndexOf(T item, int index)
public int LastIndexOf(T item, int index, int count)

But as soon as you start looking inside the code, you can realize that most of them are implemented using other ones, either just adding some default parameter values, checking what is the return value they produce or passing the program flow to Array.IndexOf/Array.LastIndexOf methods. At the end there are just 5 methods which actually do something interesting:

public T Find(Predicate<T> match)
public List<T> FindAll(Predicate<T> match)
public int FindIndex(int startIndex, int count, Predicate<T> match)
public T FindLast(Predicate<T> match)
public int FindLastIndex(int startIndex, int count, Predicate<T> match)

And as you can imagine, they all are pretty straight forward. I'm gonna list just two of them here:

public T Find(Predicate<T> match)
{
    // parameter check skipped

    for (int i = 0; i < this._size; i++)
    {
        if (match(this._items[i]))
        {
            return this._items[i];
        }
    }
    return default(T);
}

public int FindIndex(int startIndex, int count, Predicate<T> match)
{
    // parameter checks skipped

    int num = startIndex + count;
    for (int i = startIndex; i < num; i++)
    {
        if (match(this._items[i]))
        {
            return i;
        }
    }
    return -1;
}

I have to say that: there is nothing interesting here! for loop, if statement and that's it. LastXXX methods look almost exactly the same. They differ only by loop variable initial value. Even FindAll does almost not differ. Of course it stores all found items in List<T> and then returns the list, but that's not surprising at all.

As you can see, there is almost nothing to talk about here. Unfortunately, we have to get used to it, because all other methods are that simple too. But that's good, isn't it?